Note
Go to the end to download the full example code.
Resampling
Resample data from one grid onto another.
Introduction
Resampling is a general term for creating a new dataset based on an existing one. This new dataset can have a different resolution, cell shape or Coordinate Reference System (CRS).
In GridKit, resampling is generally done by defining a new grid and resampling onto that new grid. In this example a DEM is read from a geotiff file. The read function returns a BoundedRectGrid object that will serve as the initial state. Several grids with different cell shapes are then defined on which the DEM data can be resampled.
from gridkit import HexGrid, RectGrid, raster_to_data_tile
dem = raster_to_data_tile(
"../../tests/data/alps_dem.tiff", bounds=(28300, 167300, 28700, 167700)
)
print(f"Original resolution in (dx, dy): ({dem.grid.dx}, {dem.grid.dy})")
/tmp/gridkit_docs/v1.0.1/gridkit-py/gridkit/io.py:301: UserWarning: The data type '0.0' cannot be safely converted into 'int16' for file ../../tests/data/alps_dem.tiff. Falling back to unsafe cast. Consider fixing the nodata value in the metadata of the file.
warnings.warn(
Original resolution in (dx, dy): (2.0, 2.0)
Warning
Be mindful of the projection of your dataset. This dataset is in ETRS89, which is defined in degrees, which can introduce a bias. Grids defined in degrees generally do not have consistent spacing in x and y direction, meaning that one degree north is not the same distance as one degree south. It is generally recommended to work with grids defined in a local CRS that is not defined in degrees but either meters or feet.
Resampling onto the a grid
Now we have read the DEM, we can define a new grid and resample onto it Let’s define a coarser grid, effectively downsampling the data. The reason for this is that we can better compare grids if we can actually distinguish the cells. Let’s define a rectangular grid with a cell size of 10x10 degrees. I am calling it rectdem for later on I will define hexagonal ones as well. To make sure it worked we can print out the cellsize after resampling
rectdem = dem.resample(RectGrid(dx=10, dy=10, crs=dem.grid.crs), method="linear")
print(f"Downsampled resolution in (dx, dy): ({rectdem.grid.dx}, {rectdem.grid.dy})")
Downsampled resolution in (dx, dy): (10, 10)
Let’s plot the data to see what it looks like after downsampling
import matplotlib.pyplot as plt
plt.imshow(rectdem, extent=rectdem.mpl_extent, cmap="terrain")
plt.show()
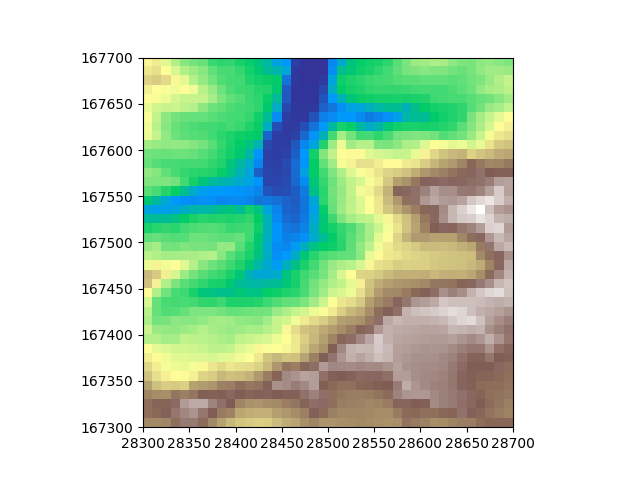
Now let’s do the same, but on hexagonal grids. There are two flavours, “pointy” and “flat” hexagonal grids. Let’s show both so we can compare them both to each other and to the downsampled rectangular grid. We can define the hexagon cell size to have the same area as the downsampled rectangular dem cell size for a fair visual comparison.
hexdem_flat = dem.resample(
HexGrid(area=rectdem.grid.area, shape="flat", crs=dem.grid.crs), method="linear"
)
hexdem_pointy = dem.resample(
HexGrid(area=rectdem.grid.area, shape="pointy", crs=dem.grid.crs), method="linear"
)
from shapely import Polygon
Now let’s create two new figures and populate these with the colored shapes of the two downsampled hexagon grids.
Since there is no ‘imshow’ equivalent for hexagons in matplotlib, we use our own gridkit.doc_utils.plot_polygons()
function, which is less performant but works on generalized shapes.
from gridkit.doc_utils import plot_polygons
# define two new figures
def plot_flat_and_pointy(flat_tile, pointy_tile):
fig_flat, ax_flat = plt.subplots()
fig_pointy, ax_pointy = plt.subplots()
plot_polygons( # Plot 1, show data
flat_tile.to_shapely(),
colors=hexdem_flat.to_numpy().ravel(),
cmap="terrain",
add_colorbar=True,
ax=ax_flat,
)
plot_polygons( # Plot 1, show tile bounds
Polygon(flat_tile.corners()),
colors="red",
fill=False,
ax=ax_flat,
)
plot_polygons( # Plot 2, show data
pointy_tile.to_shapely(),
colors=hexdem_pointy.to_numpy().ravel(),
cmap="terrain",
add_colorbar=True,
ax=ax_pointy,
)
plot_polygons( # Plot 2, show tile bounds
Polygon(pointy_tile.corners()),
colors="red",
fill=False,
ax=ax_pointy,
)
ax_flat.set_aspect("equal")
ax_pointy.set_aspect("equal")
plt.show()
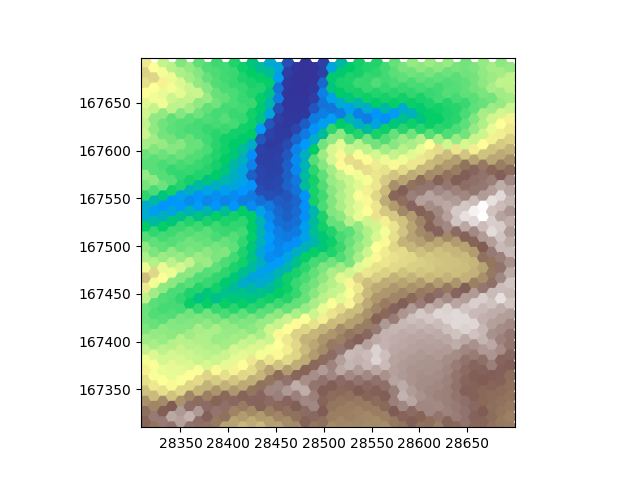
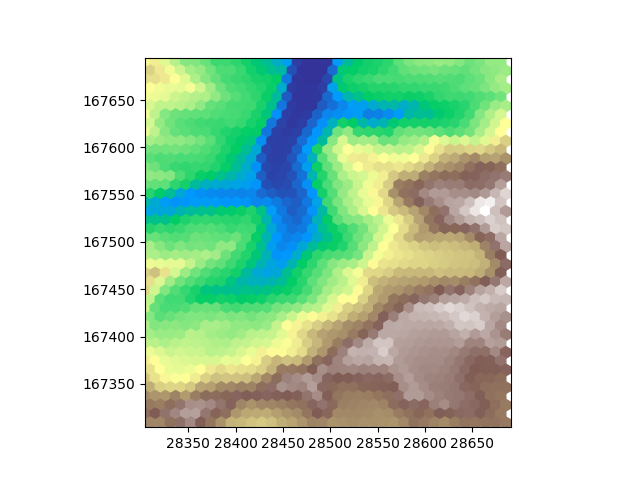
plot_flat_and_pointy(hexdem_flat, hexdem_pointy)
/tmp/gridkit_docs/v1.0.1/gridkit-py/gridkit/doc_utils.py:157: UserWarning: Adding colorbar to a different Figure <Figure size 640x480 with 2 Axes> than <Figure size 640x480 with 1 Axes> which fig.colorbar is called on.
plt.colorbar(im)
When observing these plots it is obvious that one of them has something weird going on at the edge of the tile. Triangluar and hexagonal grids both have one of the axes that is irregular. Sometimes it works out such that an irregular row or column has some cells inside the tile and some outside. In such a case we can have nodata values at the edges. The original dem file has the nodata value set to 0. The nodata value is inherited when resampling. We see these 0 values here at the edges. Matplotlib recognizes NaN values as nodata but just shows 0 values, as it should. Of course this not only affects the sides of the plot but also changes the range of the colormap. For visualization we can set the nodata_value of our dems to NaN, which will replace all occurences of a nodata value in our tile with the new nodata value.
Note
The edges can also contain nodata_values if the interpolation method looks at neighboring cells, such as with bilinear resampling. If one of the neighbours of a cell is outside of the tile, the interpolation result will also be a nodata_value, even if the cell itself is inside of the tile.
# numpy.nan also works but since that is not imported in this example, I use python's buildin nan float
hexdem_flat.nodata_value = float("nan")
hexdem_pointy.nodata_value = float("nan")
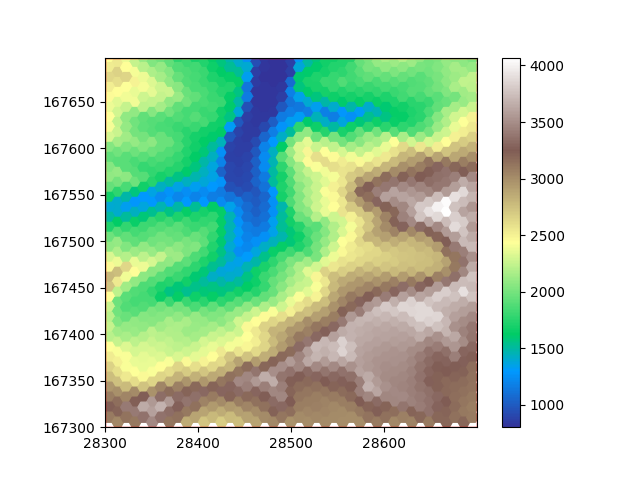
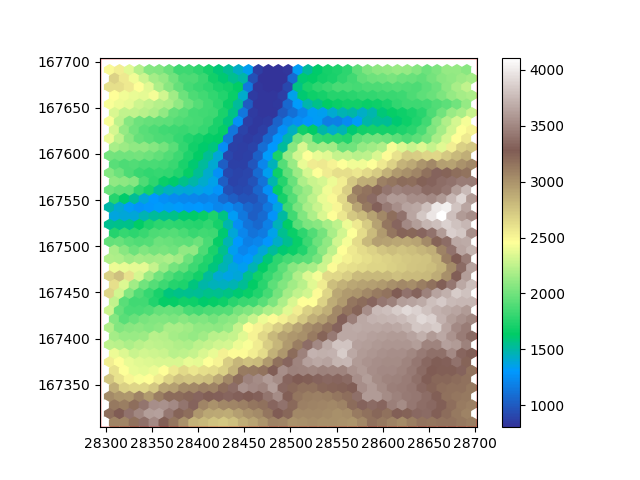
plot_flat_and_pointy(hexdem_flat, hexdem_pointy)
This concludes the example. Naturally, this example can also be used to upsample your data.
Note
The three resampled images in this example look different, but they are all equally ‘correct’. The visual difference results from the difference in positioning of the cells. Generally hexagon grids better represent rounded features, whereas rectangular grids are generally easier to work with and are more widespread.
Total running time of the script: (0 minutes 1.137 seconds)