Interpolate from points

Fill a BoundedGrid based on point data

Introduction

In this example a BoundedGrid is created from a set of points by interpolating between the points. For this operation we need:

1. locations of the points

2. values of the points

3. a grid to interpolate on

In this example, we simulate the point data using a 2d sinusoidal equation. We sample the equation at pseudo-random locations.

import numpy

numpy.random.seed(0)
x = 100 * numpy.random.rand(100)
numpy.random.seed(1)
y = 100 * numpy.random.rand(100)
values = numpy.sin(x / (10 * numpy.pi)) * numpy.sin(y / (10 * numpy.pi))
points = numpy.array([x, y]).T

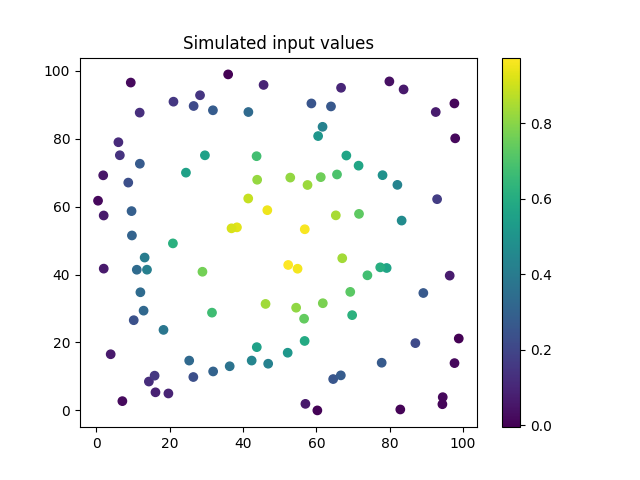
This input data looks as follows:

import matplotlib.pyplot as plt

plt.scatter(x, y, c=values)
plt.colorbar()
plt.title("Simulated input values")
plt.show()

Now we can create a grid and interpolate onto that grid.

from gridkit import HexGrid

empty_grid = HexGrid(size=6, shape="pointy")
data_grid = empty_grid.interp_from_points(points, values)

from matplotlib.patches import Rectangle

Currently the interpolation methods “nearest”, “linear” and “cubic” are supported, based on scpiy’s NearestNDInterpolator, LinearNDInterpolator and CloughTocher2DInterpolator, respectively. Here we try each method and plot them next to each other to compare.

from gridkit.doc_utils import plot_polygons

fig, axes = plt.subplots(1, 3, sharey=True, figsize=(12, 5))

for ax, method in zip(axes, ("nearest", "linear", "cubic")):
    data_grid = empty_grid.interp_from_points(
        points,
        values,
        method=method,
    )

    # plot the interpolated values at the cells
    plot_polygons(data_grid.to_shapely(), data_grid.data.ravel(), "viridis", ax=ax)

    # plot original data
    ax.scatter(x, y, c=values, edgecolors="black")

    # add outline of the grid bounds
    b = data_grid.bounds
    rect = Rectangle(
        (b[0], b[1]),
        b[2] - b[0],
        b[3] - b[1],
        linewidth=1,
        edgecolor="r",
        facecolor="none",
    )
    ax.add_patch(rect)

    ax.set_title(method, fontdict={"fontsize": 30})

fig.tight_layout()
plt.show()

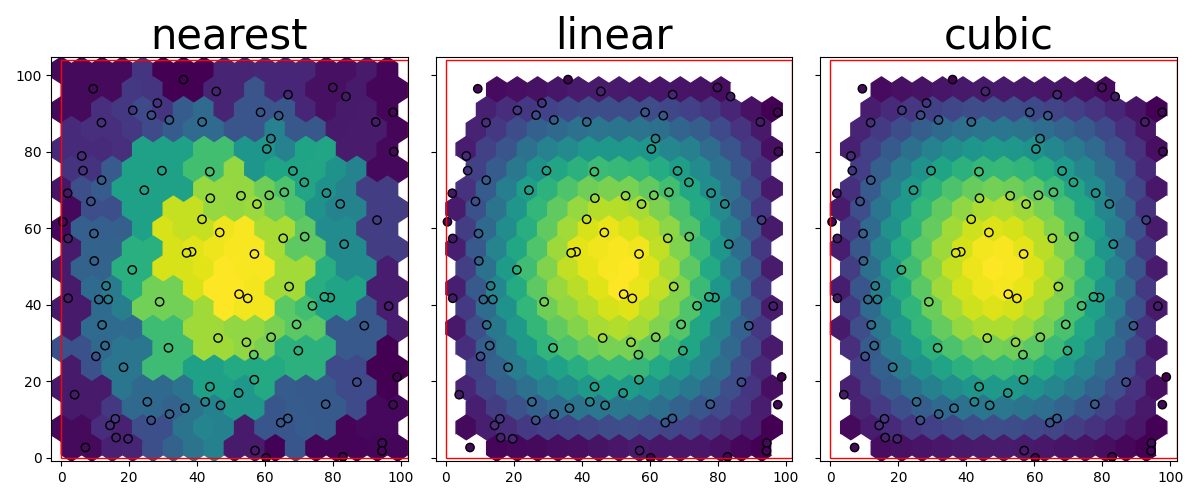
In this example, the cubic interpolation represents the original function the best, but this will differ per usecase. Note how the BoundedGrid has nodata values at the border in the “linear” and “cubic” cases. The bounds of the grid are automatically chosen to align with the supplied grid and accommodate all points. Cells of which the center is not within the convex hull of the data, but are within the selected bounds, get a nodata_value as specified in interp_from_points (default numpy.nan).