Hexagon grids

Adjusting shapes and sizes

Introduction

In this example a variety of hexagonal grids is created and compared. The goal of this exercise is to familiarize the reader with the various configurations of hexagonal grids and how they compare to one another.

Let’s create a grid and obtain the polygons in some area of interest.

from gridkit import HexGrid

# create a grid
main_grid = HexGrid(size=10, shape="pointy")

# define an area of interest, slightly larger than what we want to plot
bounds = (-20, -20, 20, 20)


def get_shapes_in_bounds(grid, bounds):
    """Return the cells of a grid in the specified bounds as a multipolygon"""
    aligned_bounds = grid.align_bounds(bounds)
    cell_ids = grid.cells_in_bounds(aligned_bounds)
    return grid.to_shapely(cell_ids, as_multipolygon=True)


main_shapes = get_shapes_in_bounds(main_grid, bounds)

Now we have shapes representing some of the cells in the grid. Let’s plot the shapes to see what we are dealing with.

import matplotlib.pyplot as plt


def plot_shapes(shapes, color="orange", **kwargs):
    """Simple function to plot polygons with matplotlib"""
    for geom in shapes.geoms:
        plt.plot(*geom.exterior.xy, color=color, **kwargs)


# plot the cell outlines
plot_shapes(main_shapes, linewidth=2)
plt.grid()
plt.show()

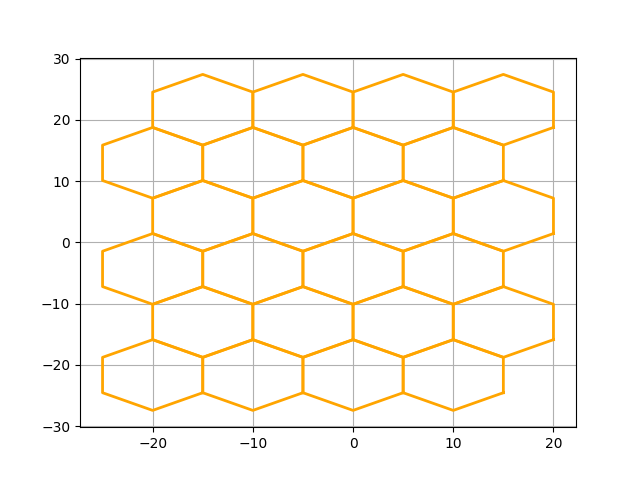
In this plot the gridlines are shown in the background to highlight how the grid is positioned in space We can modify this using the ‘offset’.

Shifting grids

Let’s shift the whole grid vertically to center it around coordinate (0,0) Also, let’s zoom in a bit to the center

main_grid.offset = (0, main_grid.dy / 2)
main_shapes = get_shapes_in_bounds(main_grid, bounds)

# plot the cell outlines
plot_shapes(main_shapes, linewidth=2)
plt.xlim(-15, 15)
plt.ylim(-15, 15)
plt.grid()
plt.show()

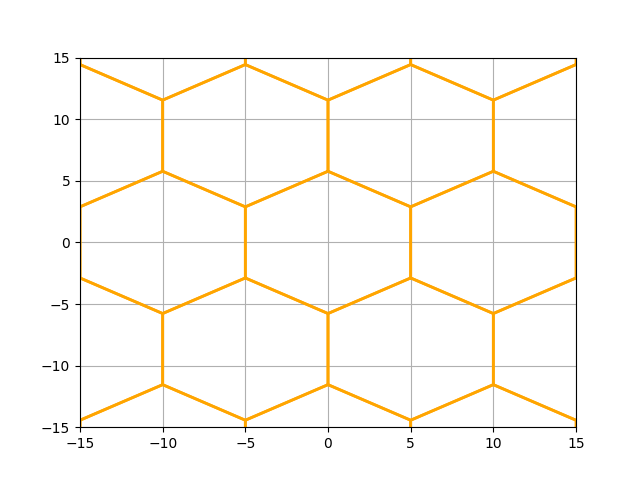
We can create a second grid and play with the size and offset If we shift the grid a deliberate amount so that it has a vertex on the center, it creates interesting patterns with respect to the grid we just created. For this we need to shift it half a ‘dx’ horizontally and half a radius (distance from center to corner) vertically, with respect to the main grid.

shifted_grid = main_grid.update(
    offset=(main_grid.dx / 2, (main_grid.dy + main_grid.r) / 2)
)
shifted_shapes = get_shapes_in_bounds(shifted_grid, bounds)

# plot the cell outlines
plot_shapes(main_shapes, linewidth=2)
plot_shapes(shifted_shapes, linewidth=2, color="purple")
plt.xlim(-15, 15)
plt.ylim(-15, 15)
plt.show()

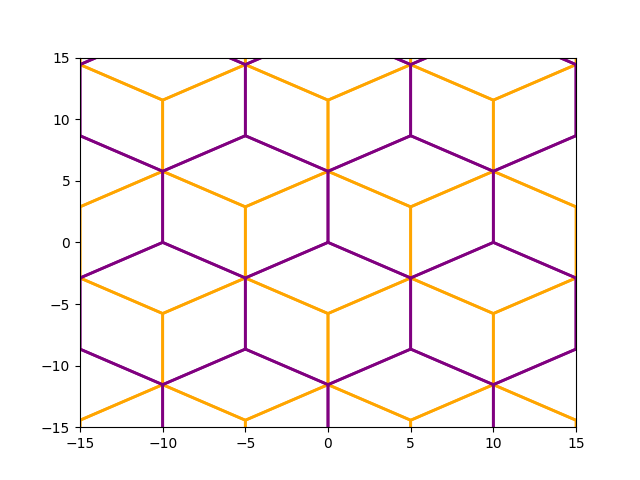
Here we were able to use the dimensions of the already existing main_grid to determine the offset of the shifted grid. It is often more convenient to first create a grid and then shift it, than it is to calculate the desired shift beforehand. The advantage of determining the offset later is that we can use the already available dx, dy and r properties of the created grid.

Grid sizes

Finally, let’s play with the size of the grid. If we keep the grids centered around zero but vary the size, we also obtain interesting patterns.

half_size_grid = main_grid.update(size=main_grid.size / 2).anchor([0, 0])
third_size_grid = main_grid.update(size=main_grid.size / 3).anchor([0, 0])

half_size_shapes = get_shapes_in_bounds(half_size_grid, bounds)
third_size_shapes = get_shapes_in_bounds(third_size_grid, bounds)

# plot the cell outlines
plot_shapes(third_size_shapes, linewidth=2, color="purple")
plot_shapes(half_size_shapes, linewidth=2, color="red")
plot_shapes(main_shapes, linewidth=2)
plt.xlim(-12, 12)
plt.ylim(-12, 12)
plt.show()

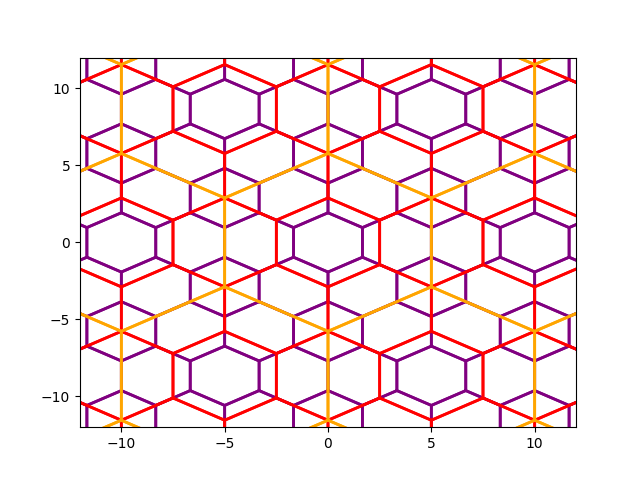
Grids that overlap and intersect in predictable ways can be utilized to select particular cells of interest. See Cell selection using other grids for a example where this is done.