Flower of life

The so called ‘flower of life’ is a type of ‘overlapping circles grid’ seen in many cultures. While it is often constructed on a triangular grid, here I will show how to construct one using three hexagonal grids where their relative offsets and rotation are chosen deliberately to construct the desired pattern.

First I will create an hexagonal grid and plot the cells as circles where the radius will be the distance from the center to a corner.

I will anchor a corner to a chosen center such that it is easier to reason about.

from gridkit import HexGrid

center = [0, 0]
depth = 3

grid = HexGrid(size=1, rotation=0).anchor(center)


def get_centroids(grid):
    """Get the centroids of a collection of cells around the specified 'center'
    at a specified depth"""
    ids = grid.neighbours(
        grid.cell_at_point(center), depth=depth, include_selected=True
    )
    return grid.centroid(ids)


grid.anchor(center, in_place=True, cell_element="corner")
centroids = get_centroids(grid)

Now I will plot the circles at the obtained centroids.

Tip

The circles are plotted as matplotlib’s PatchCollection objects. In this script I represent them as shapely Polygons for convenience and reusability, but they can also be represented using a matplotlib.circle(centroid, radius)

import matplotlib.pyplot as plt
from shapely.geometry import MultiPolygon, Point

from gridkit.doc_utils import plot_polygons


def plot_circles(geoms, color):
    plot_polygons(geoms, colors=color, alpha=0.4)
    plot_polygons(geoms, colors=color, fill=False, linewidth=3)


radius = grid.r
centroids_to_polygons = lambda centroids: MultiPolygon(
    [Point(c).buffer(radius) for c in centroids]
)
circles = centroids_to_polygons(centroids)
plot_circles(circles, "cyan")
plt.scatter(*center, marker="x", color="black", s=40)
plt.show()

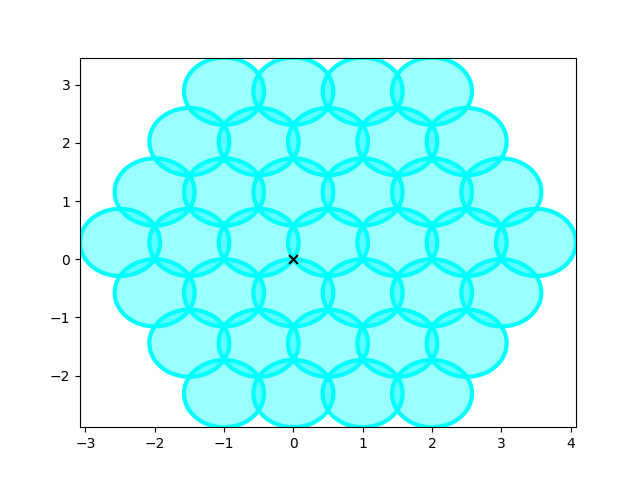
If you are familiar with the flower of life pattern, you might find that we are already nicely underway, but we are missing some circles. The first set of circles we might want to add, is basically the same set, but rotated by 60 degrees around the chosen center. This looks like so:

grid.rotation = 60
grid.anchor(
    center, in_place=True, cell_element="corner"
)  # re-anchor a corner at the chosen center after rotation
centroids1 = get_centroids(grid)
circles1 = centroids_to_polygons(centroids1)

# Plot the two sets of circles
plot_circles(circles, "red")
plot_circles(circles1, "cyan")
plt.scatter(*center, marker="x", color="black", s=40)
ax = plt.gca()
ax.set_xlim(-3, 3.5)
ax.set_ylim(-3, 3.5)
plt.show()

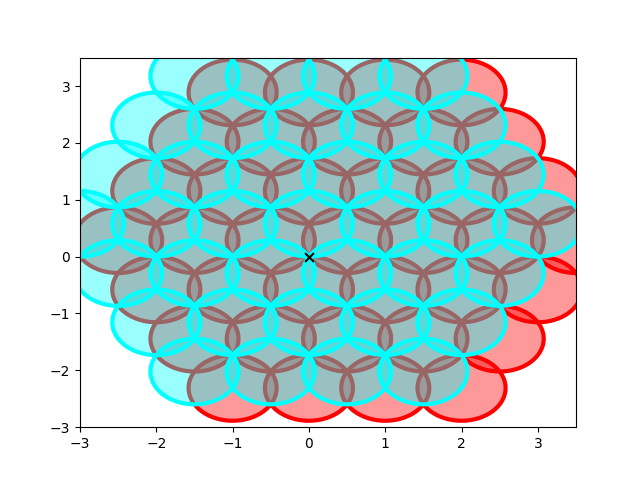
Now we are very close, but still missing some circles. The last set will need to circle the chosen center and not cross it. Let’s add the last set of circles:

grid.anchor(center, in_place=True, cell_element="centroid")
centroids2 = get_centroids(grid)
circles2 = centroids_to_polygons(centroids2)

plot_circles(circles, "red")
plot_circles(circles1, "cyan")
plot_circles(circles2, "yellow")
plt.scatter(*center, marker="x", color="black", s=40)
ax = plt.gca()
ax.set_aspect("equal")
ax.set_xlim(-3, 3.5)
ax.set_ylim(-3, 3.5)
plt.show()

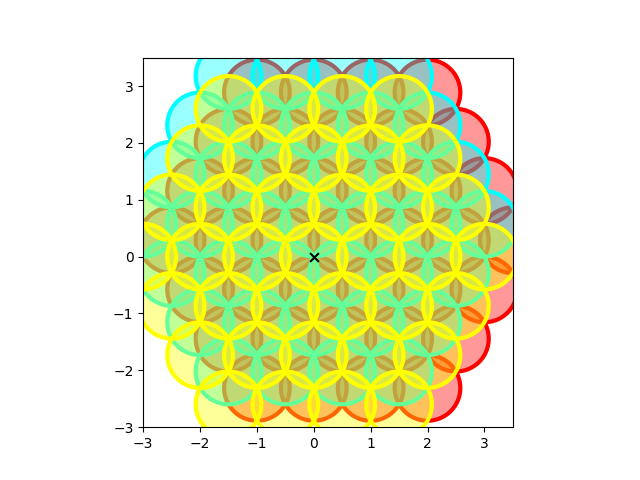
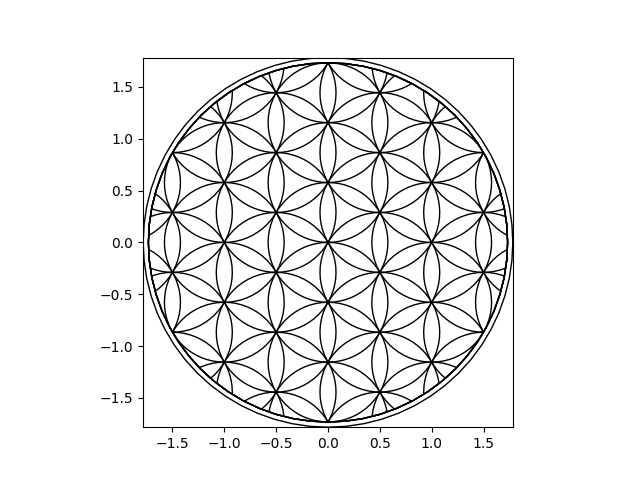
This is it! To visualize it nicely we can add a border around it and clip the polygons such that they do not cross the outer border.

outer_poly = Point(center).buffer(3 * grid.r)

all_circles = [*circles.geoms, *circles1.geoms, *circles2.geoms]
all_circles = MultiPolygon([c.intersection(outer_poly) for c in all_circles])

plot_polygons(all_circles, fill=False, colors="black")
plot_polygons(outer_poly.buffer(0.0), fill=False, colors="black")
plot_polygons(outer_poly.buffer(0.05), fill=False, colors="black")
plt.gca().set_aspect("equal")
plt.show()